Metodología para clasificación¶
Indepedientemente del método utilizado, existen etapas comunes para poder hacer aprendizaje supervisado (en particular, clasificación).
¿Cuál es nuestra tarea?: dado un conjunto $X$ de instancias, cada una de ellas con una clase $y$ asociada, queremos construir una función de clasificación que, dada una instancia nueva, nos devuelva su clase.
Algunas preguntas: ¿cómo aprendo la función?, ¿sobre qué instancias?, ¿cómo evalúo la performance de la función?
Fase 1: Preprocesamiento¶
Preprocesamiento¶
Vamos a suponer que, para poder entrenar un clasificador, debemos partir de un conjunto $D = \{(x_i,y_i)\}$, llamado conjunto de entrenamiento, donde cada instancia $x_i \in \mathbb{R}^n$ y $y_i \in \mathbb{R}$ (no todos los algoritmos de aprendizaje necesitan este formato de entrada, es solamente para fijar ideas)
(Des) afortunadamente, los conjuntos de datos que generalmente disponemos surgen de sensores, datos ingresados por humanos, fuentes diferentes, etc. Por lo tanto, debemos limpiarlos (data cleaning).
El formato de los datos originales puede ser diverso: elementos de un conjunto (categóricos), fechas, textos, imágenes, etc. Debemos buscar formas para convertirlos a un formato aceptable por el algoritmo (data transformation).
Preprocesamiento¶
Nuestros datos pueden venir de diferentes fuentes, debemos integrarlos (data integration)
Puede que, para ser más eficientes en los tiempos de aprendizaje, sea necesario agrupar datos, eliminar atributos o reducir el numero de instancias, buscando no perder infromación (data reduction)

Preprocesamiento - Valores faltantes¶
Opción 1: eliminar instancias. Problema: reduce el dataset.
Opción 2: asignar un valor especial (UNK, -1, 0, etc). Esto indica que, si faltan datos, quiere decir algo.
Opción 3: asignar el valor medio (o la mediana, o la moda) del atributo en el conjunto de entrenamiento.
Opción 4: asignar según el método de aprendizaje que estemos utilizando
Preprocesamiento - Atributos categóricos¶
Los atributos categóricos son atributos cuyos valores pertenecen a un conjunto discreto y finito (y, a veces, no numérico)
Opción 1: Cuando tenemos $n$ etiquetas, convertir a valores enteros en el rango $[0.. n-1]$. Problema: sigue siendo discreto, e induce un orden entre las etiquetas. Lo primero puede puede perjudicar a algoritmos que asumen valores continuos, lo segundo puede no representar la realidad.
Opción 2: one-hot-encoding. Creamos tantos atributos nuevos como etiquetas diferentes haya. En cada instancia, si el valor del atributo original es $i$, el atributo correspondiente al $i$-ésimo valor valdrá 1, y el resto valdrán 0.
Ingeniería de atributos - Textos¶
- ¿Cómo obtenemos atributos a partir de un texto? (Esto es toda un área, el Procesamiento de Lenguaje Natural)
- Método tradicional: Bag of Words (BOW): a partir de un vocabulario (lista de palabras del lenguaje),
construimos un vector con un atributo por palabra.
Posibles Valores para cada atributo:
- 1/0: 1 indica que la palabra existe en el texto, 0 que no.
- Cantidad de ocurrencias de la palabra en el texto (eventualmente normalizada, dividiendo sobre el total de palabras del documento)
- tf-idf: pondera la frecuencia de la palabra viendo qué tan común es en general (un valor alto indica que la palabra es común en el texto de la instancia, pero rara en el dataset).
- $ tf = \frac{count}{total}$, siendo $count$ el número de ocurrencias de la palabra en el texto, y $total$ el número total de palabras en el texto
- $ idf = \log\frac{N}{n}$, siendo $N$ el número de instancias del conjunto, y $n$ el número de instancias donde la palabra aparece en el texto
- $tf.idf = td \times idf$
Ingeniería de atributos - Textos¶
Antes crear los vectores, es usual preprocesar el texto: dividir en tokens, eliminar palabras muy comunes (stop words), hacer lematización (buscar representantes comunes a varias palabras relacionadas).
El enfoque BOW no tiene en cuenta el orden de las palabras. Una mejora: utilizar n-gramas (secuencias de n palabras). A este enfoque se lo llama también bag-of-ngrams.
Word embeddings: se generan vectores densors de baja dimensionalidad (50-200 atributos), y con algunas propiedades interesantes, a partir del contexto en el que aparece cada palabra usualmente. Los métodos más conocidos son Word2Vec y Glove.
Fase 2: División del Conjunto de Datos¶
Conjunto de entrenamiento, testeo, [y validación]¶

Debemos asegurar, para evitar el sobreajuste (overfitting), que la evaluación del modelo se realice en un conjunto de datos distinto a aquel sobre el cual se entrenó.
Sobreajuste: nuestro modelo tiene buen rendimiento sobre el dataset de entrenamiento, pero sus resultados son inferiores cuando se encuentra a datos no vistos previamente. Causa probable: el modelo está memorizando los datos de entrenamiento, sin poder generalizar.
Si evaluamos sobre el mismo conjunto de datos sobre el que entrenamos, no podemos saber si estamos sobreajustando. Sobreajustar es el peligro mayor cuando hacemos aprendizaje automático
Conjunto de entrenamiento, testeo, [y validación]¶
Separación inicial: conjunto de entrenamiento y de evaluación.
Cuantas más instancias para entrenar tengamos, probablemente mejor será nuestro modelo, PERO...
Cuantas más instancias para evaluar tengamos, menor será la varianza de nuestros resultados.
Usualmente se divide en 80%-20%, o 70%-30%
Estandarización de atributos¶
Muchos algoritmos en aprendizaje automático (e.g. knn, redes neuronales, PCA) se benefician de que los atributos continuos tengan aproximadamente el mismo orden de magnitud. Esto se debe, por ejemplo, a que se utiliza la distancia euclidiana y se busca que todos los atributos "pesen" igual al calcularla. En el caso de algoritmos que utilizan descenso por gradiente, puede haber mucha diferencia en performance.
Min-max scaling: este escalado deja los valores en el rango $[0-1]$. Dado un valor $x$, obtenemos:
$ x_s = \frac{x - x_{min}}{x_{max} - x_{min}}$
siendo $x_{min}$ y $x_{max}$ los valores mínimo y máximo respectivamente en el conjunto de entrenamiento
Normalización: se escalan los atributos para que tengan las propiedades de una distribución normal estándar, con $\mu = 0$ y $\sigma = 1$.
$ x_{norm} = \frac{x_i - \mu_{i}}{s_i} $
siendo $\mu_{i}$ la media y $s_i$ la desviación estándar del conjunto de entrenamiento
Estratificación¶
Aunque no queremos que la evaluación se realice en el conjunto de entrenamiento, sí nos interesa que la distribución de los ejemplos en uno y otro sea similar.
Al hacer la división de los conjuntos, lo usual es elegir las instancias al azar, para evitar que las agrupaciones u ordenamientos presentes en el conjunto original puedan dar lugar a distribuciones distintas. (Por ejemplo, ¿qué sucedería si, para predecir supervivencia, entrenamos sobre las pasajeras mujeres en la lista del Titanic, y evaluamos sobre los hombres?).
Un paso más, especialmente importante cuando las clases objetivo están desbalanceadas (es decir, hay muchos más ejemplos de una clase que de otras), es estratificar: elegir las instancias en cada una de las subclases, obligando a que la proporción sea la misma en el corpus de entrenamiento y en el de evaluación.
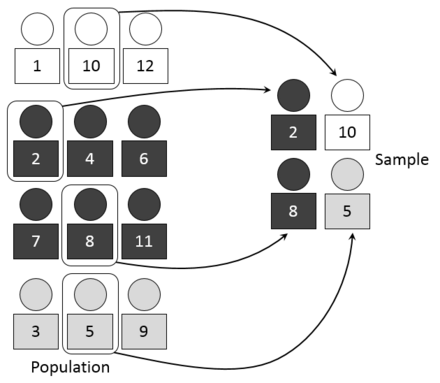
Conjunto de validación¶
Si queremos ajustar los parámetros del modelo (lo veremos en breve), no es conveniente hacerlo en el conjunto de evaluación (ya que podríamos estar sobreajustando, nuevamente).
Opción 1: separar una parte del conjunto de entrenamiento para utilizarlo en esa etapa
Opción 2: utilizar validación cruzada (cross-validation)
Fase 3: Entrenamiento¶
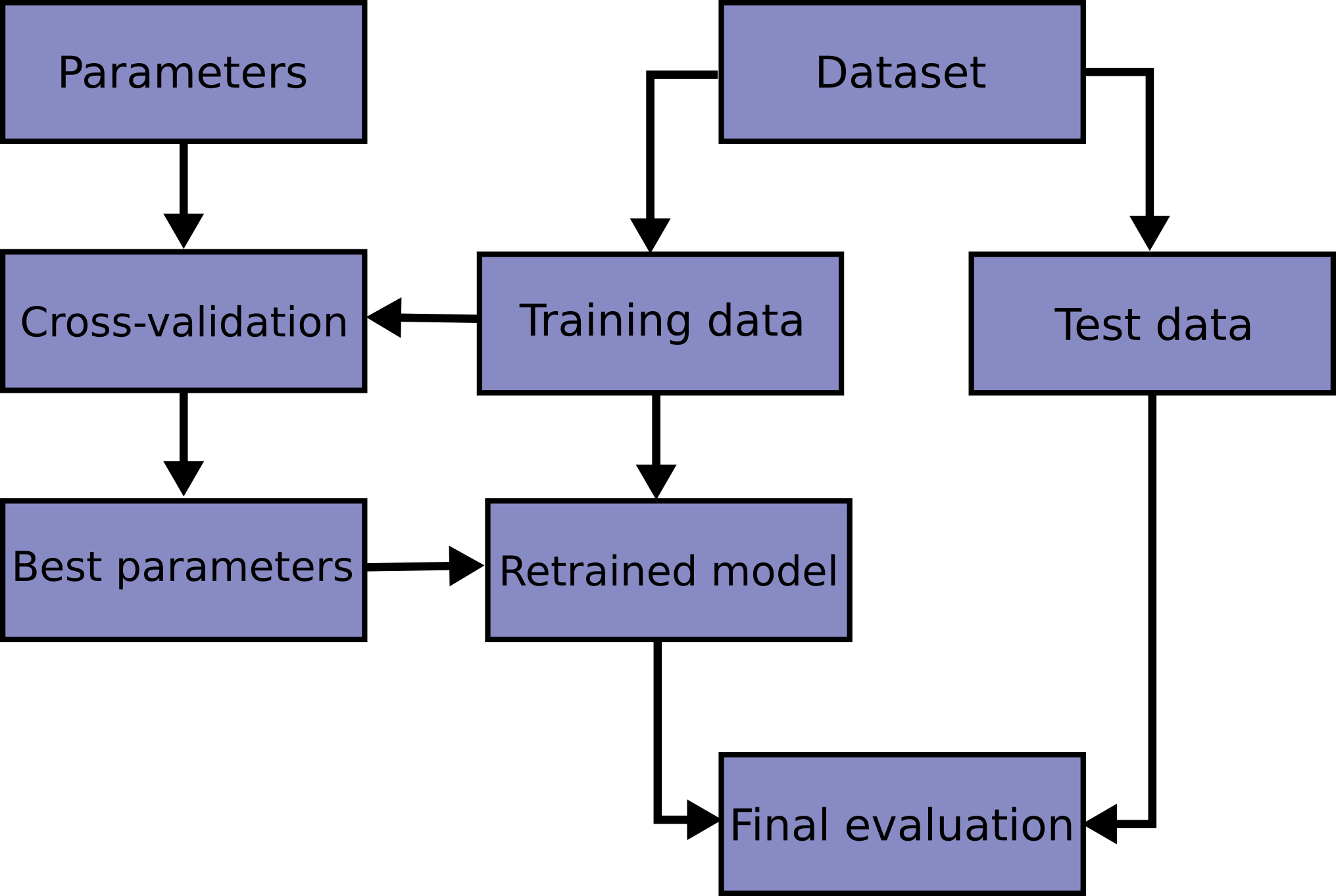
Entrenamiento¶
Durante el entrenamiento, utilizamos los datos del conjunto de entrenamiento, y un algoritmo de aprendizaje, para generar un clasificador.
Una vez generado el modelo, lo evaluamos en el conjunto de evaluación para obtener una medida de su performance (veremos más adelante las principales medidas utilizadas).
Los algoritmos de entrenamiento tienen usualmente hiperparámetros que deberían ajustarse (e.g. profundidad máxima de un árbol en los árboles decisión). Usualmente lo que se hace es probar diferentes valores para cada parámetro y ver cuál obtiene mejores resultados. Como no queremos hacer esto sobre el corpus de evaluación (¿por qué?), utilizamos un subconjunto del corpus de entrenamiento, el corpus de validación (o corpus held-out).
Validación cruzada y selección de modelos¶
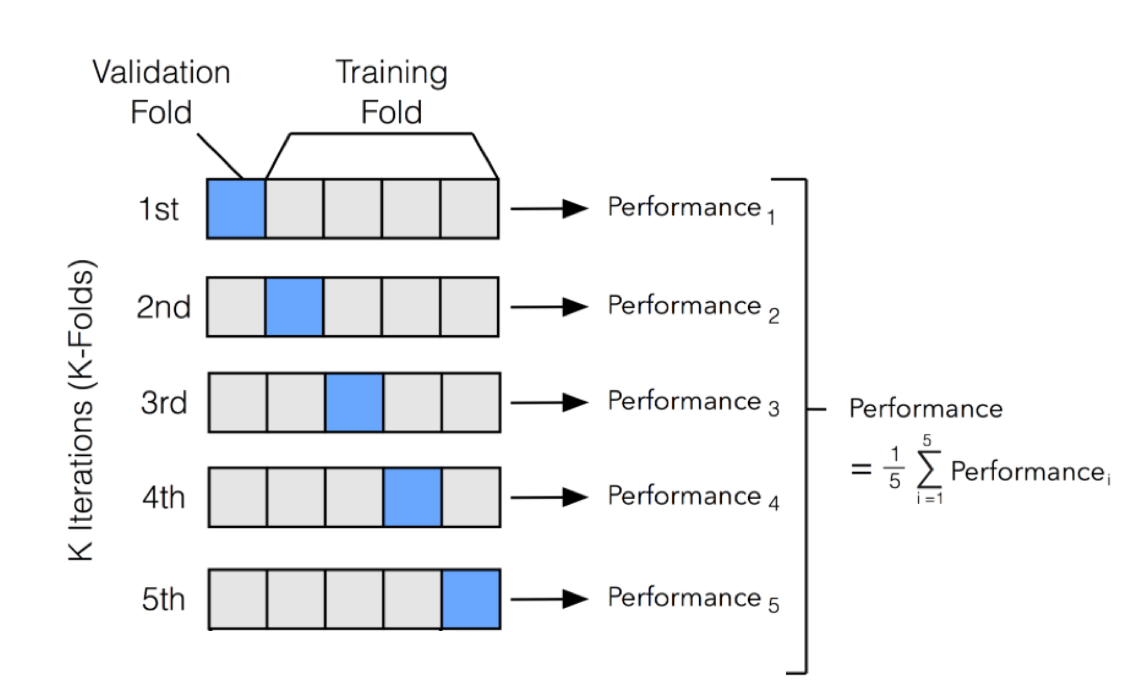
- Para utilizar mejor el corpus de entrenamiento y no tener que separar datos para validación, una alternativa es realizar validación cruzada. Este método, además, permite disminuir la varianza de los resultados (ya que se obtiene como el promedio de varias evaluaciones), aunque es más costoso en términos de tiempo de entrenamiento.
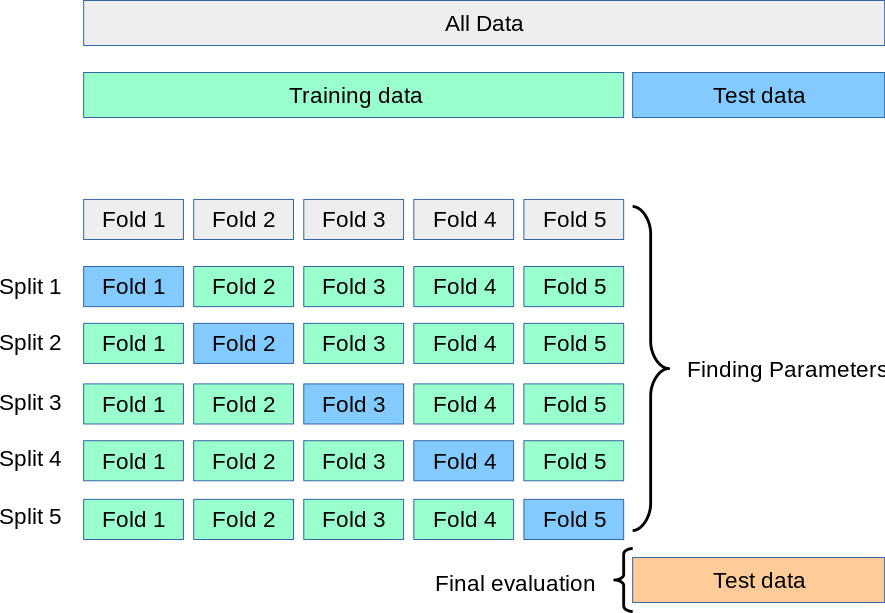
Validación cruzada y selección de modelos¶
En la validación cruzada, se divide el dataset de entrenamiento en k partes, y se utilizan (k-1) partes para entrenar, y la restante para evaluar el modelo. Este proceso se repite cambiando la parte elegida.
Se devuelve el promedio del valor de performance obtenido, y también la desviación estándar de los resultados.
Selección de atributos¶
Luego de que tenemos atributos "candidatos", nos gustaría quedarnos con aquellos que "valen la pena" para la tarea de clasificación que intentamos hacer. No hay una definición obvia de "vale la pena", pero nos interesan (para evitar ruido, y también por razones de eficiencia computacional) aquellos atributos que, en conjunto, sirvan para mejorar nuestra predicción.
El objetivo de la selección de atributos es eliminar atributos que son irrelevantes o redundantes. Por ejemplo: si tenemos dos atributos con valores idénticos, podemos eliminar uno de ellos. O si un atributo tiene siempre el mismo valor. O, por el contrario, todos sus valores son diferentes (en este caso, servirá como predictor perfecto de la clase objetivo si lo memorizamos, pero seguramente su capacidad de generalización será nula).
Fase 4: Evaluación¶
El paso final es evaluar la performance del modelo (clasificador) obtenido sobre un conjunto de datos no vistos previamente. Hasta ahora, no hemos dicho cómo medimos esa performance
Imaginemos un clasificador binario.

Accuracy¶
- Lo más sencillo es estimar el acierto (accuracy) o el error.
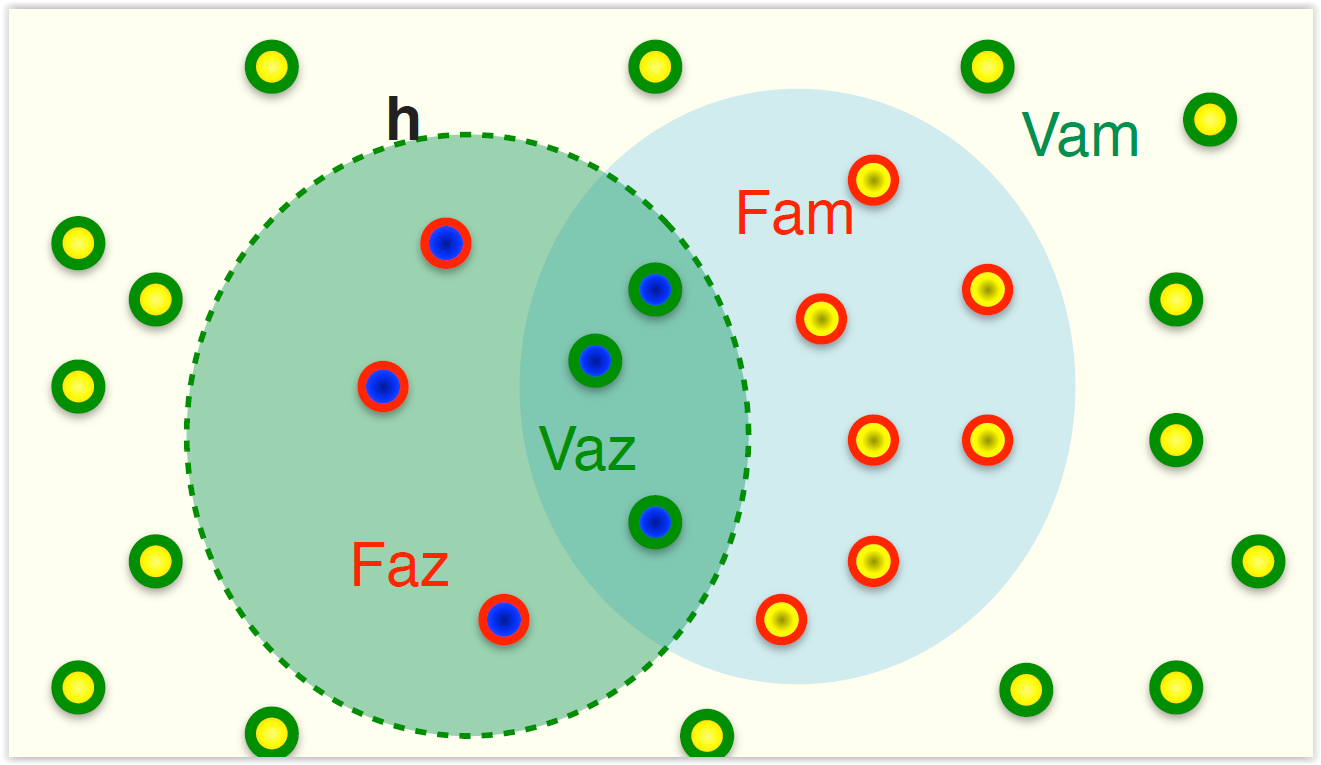 $$ acc = \frac{V_{azul} + V_{amarillo}}{V_{azul}+V_{amarillo} + F_{azul}+F_{amarillo}}$$$$ error = \frac{F_{azul} + F_{amarillo}}{V_{azul}+V_{amarillo} + F_{azul}+F_{amarillo}} = 1 - acc $$
$$ acc = \frac{V_{azul} + V_{amarillo}}{V_{azul}+V_{amarillo} + F_{azul}+F_{amarillo}}$$$$ error = \frac{F_{azul} + F_{amarillo}}{V_{azul}+V_{amarillo} + F_{azul}+F_{amarillo}} = 1 - acc $$
En nuestro ejemplo:
- Los azules (+) son 10
- Los amarillos (-) son 19
Nuestro clasificador predice:
- A 3 de los azules los predice como azules (Verdaderos Positivos)
- A 3 de los amarillos los predice como azules (Falsos Positivos)
- A 16 de los amarillos los predice como amarillos (Verdaderos Negativos)
- A 7 de los azules los predice como amarillos (Falsos Negativos)
Podemos resumir esto a través de una matriz de confusión:
| Real\Predicha | Azul (+) | Amarillo (-) |
|---|---|---|
| Azul (+) | 3 (VP) | 7 (FN) |
| Amarillo (-) | 3 (FP) | 16 (VN) |
Entonces $ acc = \frac{VP + VN}{VP+FP+VN+FN} = \frac{3+16}{3+3+16+7}= \frac{19}{29} = 0.655 $
Precisión y Recuperación¶
- El problema con el acierto y el error es que no tienen en cuenta el
comportamiento en las distintas clases.
- Si el 99% de las instancias son azules, la función constante azul tiene
un acierto de 99%.
- Se buscan alternativas para medir por clase: precisión, recuperación (recall)
Precisión y Recuperación (Recall)¶
La precision mide qué tan bueno es el clasificador cuando dice que un ejemplo es positivo
La recuperación mide qué proporción encuentra de los positivos existentes
Medida-F¶
- Combinando precisión y recuperación se obtiene la medida-F (donde $\beta$ indica cuánta más importancia se le da al recall respecto a la precisión) :
- En el caso de $F_1$, la formula queda reducida a:
- La medida-F es la media armónica entre precisión y recall, e intenta combinar ambas en un sólo número.
Medida-F¶
Ejercicio: complete la siguiente tabla, para una clasificación sobre 100.000 instancias
| $V_p$ | $F_p$ | $F_n$ | $V_n$ | Prec | Recall | $F_1$ | Accuracy |
|---|---|---|---|---|---|---|---|
| 25 | 0 | 125 | 99850 | ||||
| 50 | 100 | 100 | 99750 | ||||
| 75 | 150 | 75 | 99700 | ||||
| 100 | 50 | 50 | 99800 | ||||
| 150 | 100 | 0 | 99750 |
Medida-F¶
Ejercicio: complete la siguiente tabla, para una clasificación sobre 100.000 instancias
| $V_p$ | $F_p$ | $F_n$ | $V_n$ | Prec | Recall | $F_1$ | Accuracy |
|---|---|---|---|---|---|---|---|
| 25 | 0 | 125 | 99850 | 1.00 | 0.17 | 0.29 | 0.999 |
| 50 | 100 | 100 | 99750 | 0.33 | 0.33 | 0.33 | 0.999 |
| 75 | 150 | 75 | 99700 | 0.33 | 0.50 | 0.40 | 0.998 |
| 100 | 50 | 50 | 99800 | 0.67 | 0.67 | 0.67 | 0.999 |
| 150 | 100 | 0 | 99750 | 0.60 | 1.00 | 0.75 | 0.999 |
- ¿Qué sucede con la accuracy? ¿Y con los otros valores? ¿Cuál de los clasificadores eligiría?
Problemas multiclase¶
¿Qué sucede cuando se tiene un problema multiclase (es decir, hay más de dos categorías)?
Las medidas anteriores siguen valiendo, si consideramos como "positivos" a las instancias que pertenecen a una clase, y "negativos" al resto (one-versus-all).
Esto nos da una medida por cada clase. Existen diferentes formas de resumir esa información:
Se calcula la medida por clase, y luego se promedia los valores obtenidos (macro average)
Se calcula la medida por clase teniendo en cuenta el aporte de instancias cada clase (micro average)
Lo usual es calcular ambas, y analizar según mi problema
Problemas multiclase¶
- Por ejemplo, supongamos que queremos calcular precisión para la siguiente tabla:
| Clase | $V_p$ | $F_p$ | Prec |
|---|---|---|---|
| A | 1 | 1 | 0.5 |
| B | 10 | 90 | 0.1 |
| C | 1 | 1 | 0.5 |
| D | 1 | 1 | 0.5 |
La macro-average será $ \frac{0.5+0.5+0.1+0.5}{4} = 0.4 $
La micro-average será $ \frac{1+10+1+1}{2+100+2+2} = 0.22 $
Puede verse que la micro-average es menor, porque lo mal que nos fue en la clase B hace que el promedio baje, porque es una clase mucho más grande que las demás.
Qué medida es más "útil", como toda medida, depende de lo que queremos evaluar:
- La micro-average da más peso a las clases grandes en el análisis general
- La macro-average permite evaluar mejor que tan "equilibrado" es el comportamiento de mi clasificador
- En lo posible, reportar ambas y analizar según mi problema
Problemas multietiqueta¶
- En un problema multietiqueta, hay más de una clase asociada a cada etiqueta, como en el siguiente ejemplo
| Instancia | Clase | Predicción |
|---|---|---|
| 1 | A,B | B,C |
| 2 | A,B,C | A,C,D |
| 3 | A,B | A,B |
Se pueden calcular las medidas utilizando solamente los ejemplos de cada clase, sin importar el resto. Esto permite utilizar las medidas mencionadas anteriormente
Se pueden aplicar otras medidas, como promediar el índice de Jaccard $IJ(A,B) = |A \cap B| / |A \cup B|$
En el ejemplo, $IJ(1)=1/3$, $IJ(2)=1/2$, $IJ(3)=1$, y por lo tanto el índice de Jaccard promedio será $0.61$
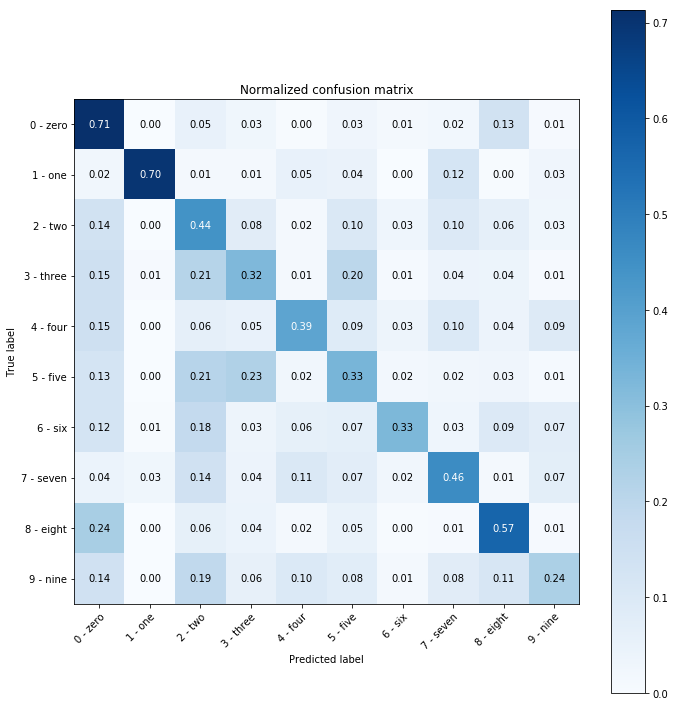
Matriz de confusión¶
Son muy útiles para intentar entender el comportamiento del clasificador, especialmente cuando se tiene más de dos clases.
Las filas de la matriz representan las instancias pertenecientes en el conjunto a cada clase, mientras que las columnas indican cómo fueron clasificadas por mi modelo.
Cada celda se lee como "X elementos de la clase {fila} fueron clasificados como {columna}
En la diagonal quedan los elementos correctamente clasificados.
Línea base y línea máxima¶
¿Cómo sabemos si el resultado que obtuvimos es "bueno", o "razonable"?
El resultado depende del problema.
Siempre es bueno tener una línea base: una solución anterior sencilla, o un clasificador que elige siempre la clase más probable o según la distribución del conjunto de entrenamiento
También es útil (si es posible) tener una línea de tope, sobre todo en problemas donde no hay antecedentes. Típicamente, se pide a humanos que actúen como clasificadores y se evalúa su performance.